In algebra, polynomial long division is an algorithm for dividing a polynomial by another polynomial of the same or lower degree, a generalised version of the familiar arithmetic technique called long division. It can be done easily by hand, because it separates an otherwise complex division problem into smaller ones.
Find
The problem is written like this:
The quotient and remainder can then be determined as follows:
- Divide the first term of the numerator by the highest term of the denominator. Place the result above the bar (x3 ÷ x = x3· x−1 = x3−1 =x2).
- Multiply the denominator by the result just obtained (the first term of the eventual quotient). Write the result under the first two terms of the numerator (x2 · (x − 3) = x3 − 3x2).
- Subtract the product just obtained from the appropriate terms of the original numerator, and write the result underneath. This can be tricky at times, because of the sign. ((x3 − 12x2) − (x3 − 3x2) = −12x2 + 3x2 = −9x2) Then, "bring down" the next term from the numerator.
- Repeat the previous three steps, except this time use the two terms that have just been written as the numerator.
- Repeat step 4. This time, there is nothing to "pull down".
The polynomial above the bar is the quotient, and the number left over (−123) is the remainder.
The long division algorithm for arithmetic can be viewed as a special case of the above algorithm.
Division transformation
Polynomial division allows for a polynomial to be written in a divisor–quotient form which is often advantageous. Consider polynomials P(x),D(x) where deg D < deg P. Then, for some quotient polynomial Q(x) and remainder polynomial R(x) with deg R < deg D,
This rearrangement is known as the division transformation, and derives from the arithmetical identity 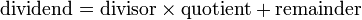 . It has a variety of applications, including the determining of a remainder after polynomial division by a polynomial of degree ≥ 2.
. It has a variety of applications, including the determining of a remainder after polynomial division by a polynomial of degree ≥ 2.
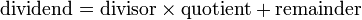 . It has a variety of applications, including the determining of a remainder after polynomial division by a polynomial of degree ≥ 2.
. It has a variety of applications, including the determining of a remainder after polynomial division by a polynomial of degree ≥ 2.Source: Wikipedia
 Labels:
Long Division
Labels:
Long Division


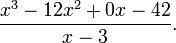


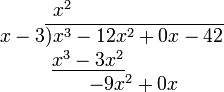
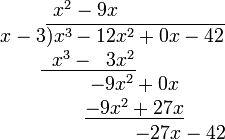
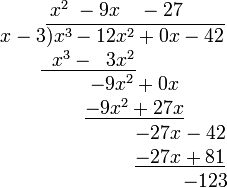

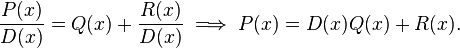
 Previous Article
Previous Article
